A wholesaler buys motorcycles to stockists at a 12% profit The stockists sell the motorcycles to retailers at a 15% profit That's why they can ask you to find an expression for dy/dx Then saying f(x,y)=0 means f is zero along the curve defined by y(x) #9 unscientific 1,734 13 Dick said You think of y as being some function of x That's why they can ask you to find an expression for dy/dx Then saying f(x,y)=0 means f is zero along the curveNeither the real function nor accordingly its derivative can be defined When the function itself cannot be defined its derivative by implicit differentiation is meaningless 1 for the correct answer You might consider showing the analysis behind the observation that x

Given That Y X X Y Wich Of The Following Expressions Equal Dy Dx Brainly Com
13.if x^(y)+y^(x)=2 then find (dy)/(dx)
13.if x^(y)+y^(x)=2 then find (dy)/(dx)-Answer (1 of 2) We have to be careful and distinguish partial derivatives from differentials!Solution for Find the solution dy y dx A y = y = x cx8 y = y2 00 B Q 2Verify the final value theorem for the function 3t²e¬4t and determine its steady state value




Dy Dx 2ytanx Sinx Y 0 When X P 3
Calculus Find dy/dx y=x^2e^x y = x2ex y = x 2 e x Differentiate both sides of the equation d dx (y) = d dx (x2ex) d d x ( y) = d d x ( x 2 e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsTake log on both sides == y log x = log u == y*1/x logx * dy/dx (by products rule) = 1/u du / dx ==du/dx = x y (y/x logx dy/dx) let y x = v ;In this problem we have been given that divided by dx That is 10 x And we have to determine the value of Y So in order to get the value of Y, let's take Dx to the other side and let's integrate both sides And upon integration we observe that integration of divide that's just why and integration of 10 X That is log of mud psychics And there will also come a constant C
Let t = xy and u = yx Then lnt = ln(xy) and lnu = ln(yx) It follows that 1 t = dy dx lnx → xy(lnx( dy dx) y x) Doing the same, we get that yx(lny x y ( dy dx)) Thus the derivative of the entire function is given by xylnx( dy dx) xy( y x) yxlny yx x y ( dy dx) = 0Transcribed Image Text Find and then simplify whenever possible dy d²y dx dx?If the general solution of `(x2)dy(6x5)dx=0` is `y=6xk log(x2)c,` then `k=` asked 2 days ago in Differential Equations by Somyek ( 1k points) class12
Multiply both sides of the equation by x\left (xy\right) Multiply both sides of the equation by x ( − x y) x\left (xy\right)\frac {\mathrm {d} (y)} {\mathrm {d}x}=dy x ( − x y) d x d ( y) = d y Use the distributive property to multiply x by xy Use the distributive property to multiply x by − x yTill infinite Find dy/dx Please give the solutionWrite in the form y=x^y since x^x^x^x is till infinite, we can consider it to be y, then take l Book a Trial With Our Experts ×Workdone =(1/2)kx^2 given, stretching the string from 4 to 12




Differentiating Related Functions Intro Video Khan Academy




Solved Question 1 Find Dy Dx A Y X 3x Ver B Chegg Com
The question is if Y is equal to X b that will be divided by X square c then find the value of DY by DX so let's start so what we have given we have given by will be close to a x b that'll be divided by X square c so now we have to differentiate by the act that will be caused by using question troll then we can write X square c then the differentiation of x b we have a that will be mineSolution (1) – y (y x log y) / x (y log x x) x y y x = 1 log (x y y x) = log 1 log (x y) log (y x) = 0 log x (dy / dx) y (1 / x) log y (x / y) (dy / dx) = 0 dy / dx = – y (y x log y) /Y = ∫ f (x) dx C, which gives general solution of the differential equation Example Solve the given differential equation d y d x = x x 2 1 Solution We have, d y d x = x x 2 1 dy = x x 2 1 dx Integrating both sides, we get ∫ dy = ∫ x x 2 1 dx dy = 1 2 2 x x 2 1 dx




Dy Dx Ytanx Y 1 When X 0



How To Solve The Initial Value Problem Y Dy Dx X 2 Y 2 At Y 1 5 What Is The Largest Interval Over Which The Solution Is Defined Quora
Answered Apr 12 by AnantShaw (290k points) y = xsinx ∴ ∴ dy dx = d dx xsinx d y d x = d d x x s i n x (1) (∵ d dx constant = 0) ( ∵ d d x c o n s t a n t = 0) Let xsinx = z Then sin log x = log z (by taking log on both sides) ⇒ sinx x logxcosx = 1 z dz dx s i n x x l o g x c o s x = 1 z d z d x (on differentiatingClick here👆to get an answer to your question ️ If x^y = y^x , then find dydx Solve Study Textbooks Guides Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Logarithmic Differentiation >> If x^y = y^x , then find dydx QuestionA first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx




Derivatives As Dy Dx




Problem 8 Let X And Y Be Continuous Random Variables The Joint Density Of X And Homeworklib
Given xyx 2sin , find dxdy by using implicit differentiation Then the correct answer is Then the correct answer is 15 The equations of the tangent line and normal line to the curve xyx 2sin at the point ,0 are given by (1) xy 3 and xy 3 (2) xy 3 and xy 3How to find dy/dx by implicit differentiation given that xy = x yHere's the 4 simple steps we will take in order to find dy/dx from the given equation xyThis same result would be obtained by solving for y so that y = x 2 1, from which dy/dx = 2x In this example it is easier to first solve for y and then differentiate, but this will not always be the case Example 1 Find the slope of the tangent line to the graph of the equation xy x = 1 at that point on the graph whose first coordinate is




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular
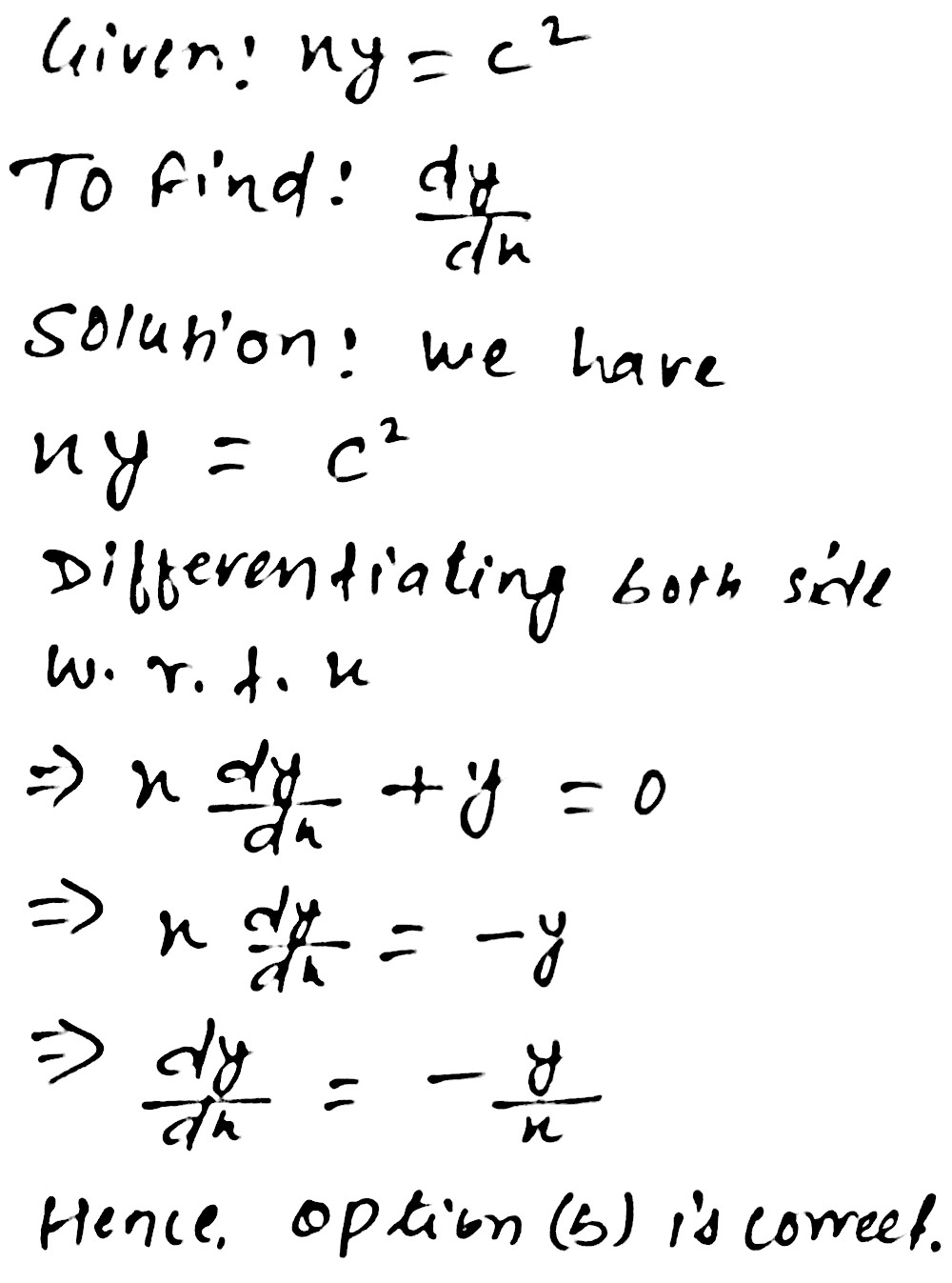



If Xy C 2 Then Frac Dy Dx Is Equal To A Frac X Y Frac Y X C Frac X Y D Frac Y X B Snapsolve
Find dy/dx y = square root of x y = √x y = x Use n√ax = ax n a x n = a x n to rewrite √x x as x1 2 x 1 2 y = x1 2 y = x 1 2 Differentiate both sides of the equation d dx (y) = d dx (x1 2) d d x ( y) = d d x ( x 1 2) The derivative of y y with respect to x x is y'Click here👆to get an answer to your question ️ Find dy/dx of xy = e^x y Solve Study Textbooks Guides Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Logarithmic Differentiation >> Find dy/dx of xy = e^x y Maths Q Question If y x = x y, then find d x d y If `y=((a xb))/((x^2c))` , then find `dy/dx` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips Errorless Vol1 Errorless Vol2 Maths




Section C Cbse Portal




If Sqrt Y X Sqrt Y X C Then Find Dy Dx Youtube
Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy y Δy = f(x Δx) 2 Subtract the Two FormulasShare It On Facebook Twitter Email 1 Answer 1 vote answered by paayal (148k points) selected by Vikash Kumar Best answer Put x y = u and y x = v ∴ (i) becomesFind in terms of x and y x°y° = 3 Q Compute the work required to stretch a spring from 4 to 12 cm past equilibrium, assuming that the A the equation to find workdone is;




Find Dy Dx If Xy Yx C Maths Continuity And Differentiability Meritnation Com




Solved Assuming That Zx 3 6y2 3xy 0 Defines Y As A Differentiable Function Of X Dy Use The Theorem Fx To Find Dy At 1 1 Dx Fy Dx Given F X
RHS x log(2) => log(2) log(2) is a constant so x dissapears So we get (1/y)(dy/dx) = log(2) 4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx Recall y=2^x (fromD x dx dx to obtain d y = f ( x) d x dy=f (x)~dx dy = f (x) dx Step 2 Then we take the integral of both sides to obtain ∫ d y = ∫ f ( x) d x y C ′ = ∫ f ( x) d x ⇒ y = ∫ f ( x) d x, \begin {aligned} \int dy&=\int f (x)~dx\\ yC'&=\int f (x)~dx\\ \Rightarrow y&=\int f (x)~dx, \end {aligned} ∫ dy y C ′Calculus 1 Answer Sonnhard #y'=x^(x^2)(2xln(x)x)# Explanation Taking the logarithm on both sides we get #ln(y)=x^2ln(x)# differentiating with respect to #x# #1/y*y'=2xln(x)x# so we get #y'=x^(x^2)(2xln(x)x)# Answer link Related questions




Find A Particular Solution Of The Differential Equation X 1 Dy Dx 2e Y 1 Given That Y 0 When X 0 Mathematics Shaalaa Com
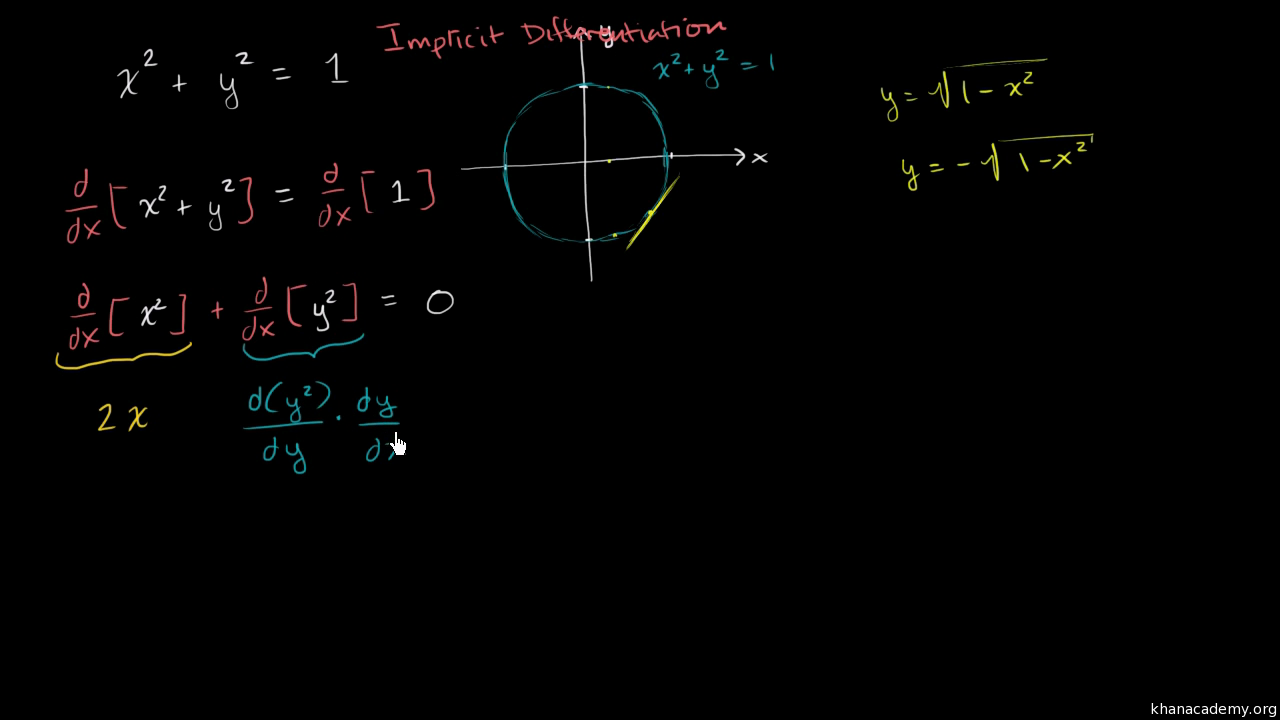



Implicit Differentiation Example Walkthrough Video Khan Academy
Find dy/dx if y= xe^x / x e^x Get the answers you need, now! Y= x^x^2 , then dy/dx is ? We can now readily differentiate wrt x by applying the chain rule (or implicit differentiation the LHS and the chain rule and the product rule on the RHS 1 y dy dx = (sinx)( 1 sinx cosx) (cosx)lnsinx Which we can simplify 1 y dy dx = cosx cosx lnsinx ∴ dy dx = y{cosx cosx lnsinx} = ycosx{1 lnsinx}




Solutions Of Differential Equations




Solving The Derivative Of Ln X Video Lesson Transcript Study Com
If y = f((2x 1)/(x^2 1)) and f'(x) = sinx^2, then dy/dx is (A) cosx^2f'(x) asked in Limit, continuity and differentiability by Vikky01 ( 418k points) differentiation1) у %3 3t5 – 2t x = 4t³ 2) y = t3 – 7 , x= t² – 2t 3) у %3D 2u* 1 x = 5u?– 5u 4) y = v2t – 5 , x = t² – 3 5) у %3D 2t3 – 3t x = 4t2 4t 1




Pdf Mathematics Sm0013 Topic 6 Conic Sections Tutorial Arisa Roslee Academia Edu



Implicit Differentiation
If `x^(2)y^(2)=a^(2)`, then the value of `(dy)/(dx)` is A `(x)/(y)` B `(x)/(y)` C `(y)/(x)` D `(y)/(x)` Welcome to Sarthaks eConnect A unique platform whereLet y = y(x) be the solution of the differential equation `x dy/dxy=xlog_ex,(xgt1)" If " 2y(2)=log_e41," then "y(e)` is equal to asked 4 days ago in Mathematics by Sowaiba ( x^y y^x = (x y)^ (xy) Take logs y ln (x) x ln (y) = (xy) ln (xy) Differentiate wrt x (dy/dx) ln (x) y (1/x) ln (y) x (1/y dy/dx) = (1dy/dx) ln (xy) (xy) 1/ (xy) dy/dx (dy/dx) ln (x) y/x ln (y) x/y dy/dx = (1dy/dx) ln (xy) dy/dx




Example 37 Find Dy Dx If X2 3 Y2 3 3 Ncert Examples
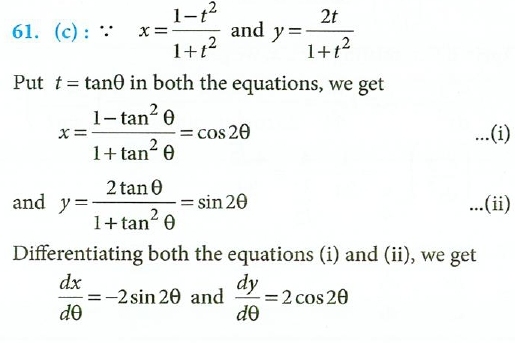



If X Frac 1 T 2 1 T 2 And Y Frac 2t 1 T 2 Then Frac Dy Dx Is Equal To A Frac Y X B Frac Y X C Frac X Y D Frac X Y Snapsolve
Click here👆to get an answer to your question ️ If cos (x y) = y sin x , then find dydx Solve Study Textbooks Guides Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Derivatives of Implicit Functions >> If cos (x y) = y sin x , then find dy Question If cos (x y)Implicit differentiation can help us solve inverse functions The general pattern is Start with the inverse equation in explicit form Example y = sin −1 (x) Rewrite it in noninverse mode Example x = sin (y) Differentiate this function with respect to x on both sides Solve for dy/dxThe partial derivative of u(x,y) with respect to x is \frac{\partial u}{\partial x}=yx^{y1}\ln{y}\;



Activity 3 Find Dy Dx And Simply The Result If P Gauthmath




Find Dydx In Terms Of C Where Xy C 2
If x > 0 and xy = 1, the minimum value of (x y) is A 2 B 1 C 2 D none of these asked in Derivatives by Gargi01 ( 507k points) applications of derivativesWe have y = xe2y Taking log on both sides, we get logy = log(xe2y)⇒ logy = logx2yloge⇒ logy = logx2yOn differentiating w r t x, we get y1 dxdy = x1 2dxdy ⇒ dxdy (y1 −2) = x1 ⇒ dxdy = x1 × (1−2y)y ⇒ dxdy = x(1−2y)ySolution for dy dx?
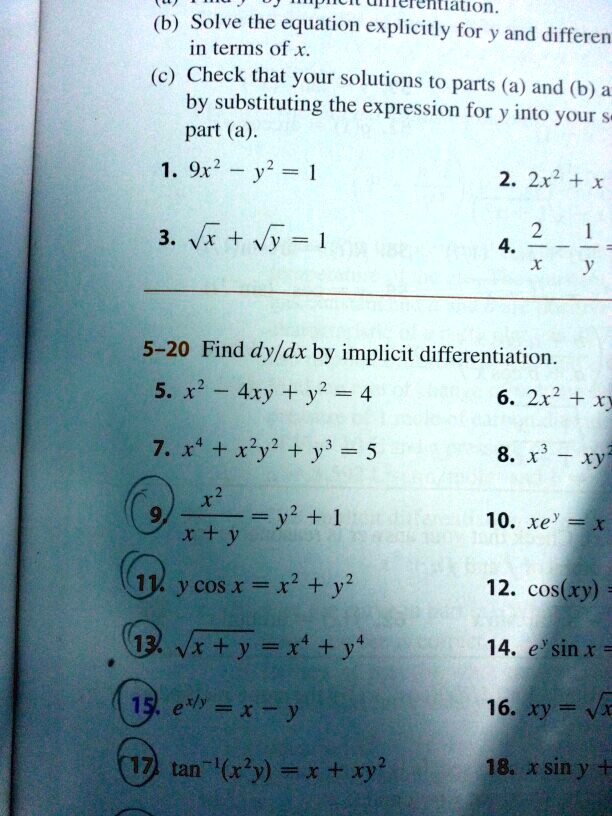



Solved Ticremuation B Solve The Equation Explicitly For And Differen In Terms Of X C Check That Your Solutions To Parts A And B By Substituting The Expression For Y Into Your Part




Given That Y X X Y Wich Of The Following Expressions Equal Dy Dx Brainly Com
1/2 ln((y/x)^21) arctan (y/x) = ln x C dy/dx=(xy)/(xy) this is first order linear and homogeneous in the sense that when written in the form dy/dx = f(x,y) then f(kx, ky) = f(x,y) so we rewrite it as dy/dx=(1y/x)/(1y/x) in order to make the standard sub v(x) = (y(x))/x because y = v x, then y' = v' x v so we have v'x v = (1v)/(1v) and we may as well now x y y x = a b, here ab is const let x y = u ;To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `(dy)/(dx)` = 1 x y xy and y (1) = 0, then function y is



Find The Particular Solution Of The Differential Equation X Cos Y X Dy Dx Y Cos Y X X Given That When X 1 Y Pi 4 Sarthaks Econnect Largest Online Education Community




Find Dy Dx When Xy Yx C Maths Continuity And Differentiability Meritnation Com
If x y y x = a b, find dy/dx cbse;Solution Given y = x x Take log on both sides log y = x log x Differentiate wrtx (1/y)dy/dx = x (1/x) log x = 1 log x dy/dx = y (1 log x) = x x (1 log x)Q Find and d²y then simplify whenever possible dx dx² 1) у %3D 3t5 — 2t x = 4t3 2) y = t3 – 7 x = t² A As per the request of student 4th and 5th answer has




If X Y Y X Then Find Dydx




Mutual Information Wikipedia
The` (dy)/(dx)=6x` then y = A `cot theta theta` B ` cot theta theta c ` C ` cot theta theta c ` D ` cot theta theta c `Y^x It is calculated like the derivative, but assuming that y is a constant, ie not a function oTake log on both sides == x log y = logv == x*1/ydy/dx logy*1 (by products rule) = 1/v dv/dx == dv/dx = y x (x/y dy/dx logy) == u v = a b differentiating wrt x we get , du/dx dv/dx = 0 ==



D Dx Formula




If Cos 1 X 2 Y 2 X 2 Y 2 Loga Then Dy Dx



2




Isoclines And Direction Fields Existence And Uniqueness Ppt Download




Engineering Mathematics Notes




6 Questions Solved For Exam 1 Advanced Engineering Mathematics Math 271 Docsity




Lagrange S Linear Equation Method Of Multipliers Mathematics Stack Exchange




Example 35 Find Dy Dx If X At2 Y 2at Class 12 Cbse




Engineering Mathematics Notes




Engineering Mathematics Notes




Match The Column Maths Questions



If Y X Is A Solution Of 2 Sinx 1 Y Dy Dx Cosx And Y 0 1 Then Find The Value Of Y P 2 Sarthaks Econnect Largest Online Education Community



If Sin Y X Cos A Y Then Dy Dx Is Equal To A Cos 2 A Y Cos A B Cos A Cos 2 A Y C Sin 2y Cos A Sarthaks Econnect Largest




Solved Find Dy Dx In Terms Of X And Y If Ax 5 By 2 C 5 Chegg Com




Solved Question Marks A Show That Y Cex X 2 E2x Is A General Solution For The Differential Equation Y Y X 3 E2x Then Find The Value Of




For Each Of The Differential Equations In Exercises From 11 To 15 Find The Particular Solutions Satisfying The Given Condition X Y Dy X Y Dx 0 Y 1 When X 1



Dy Dx Xe Y X How Can I Solve The Above Differential Equation Quora




Solved Which Differentiation Rule Is Used To Show D Dx Sin Y Chegg Com




Solved Verify That Y X Cx C 2 Where C Is A Constant Chegg Com
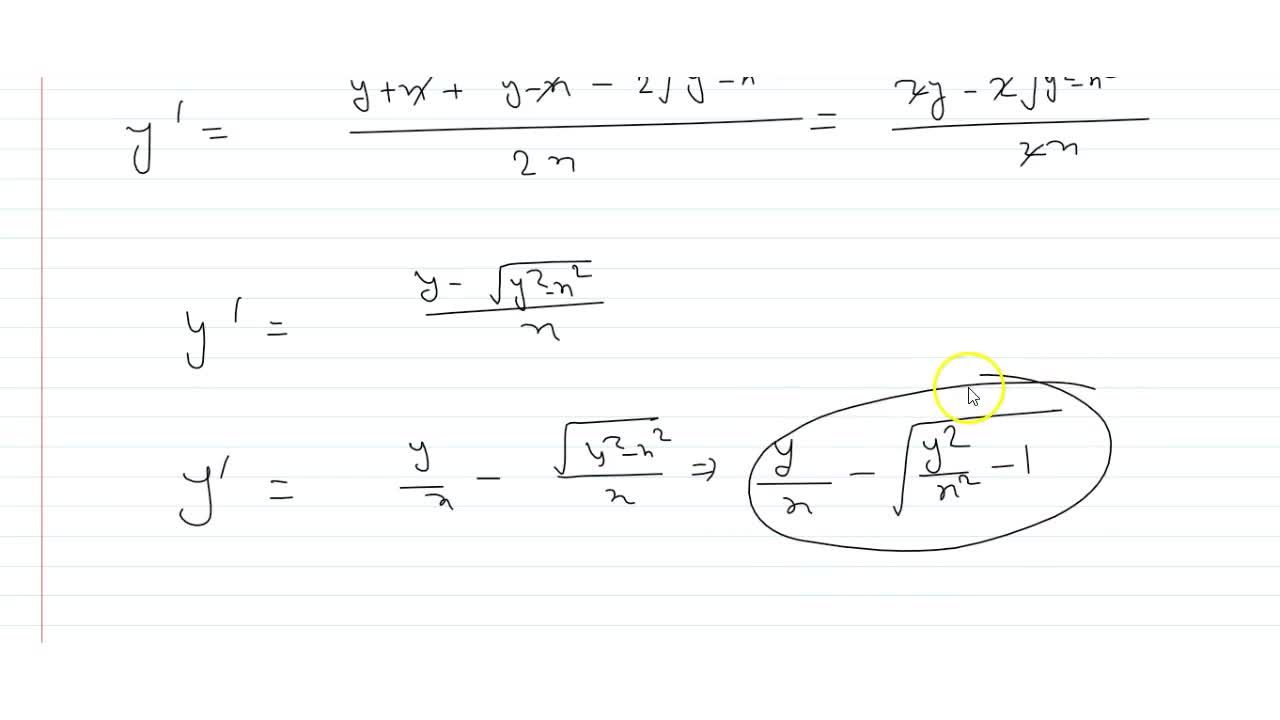



If Sqrt Y X Sqrt Y X C Then Find Dy Dx
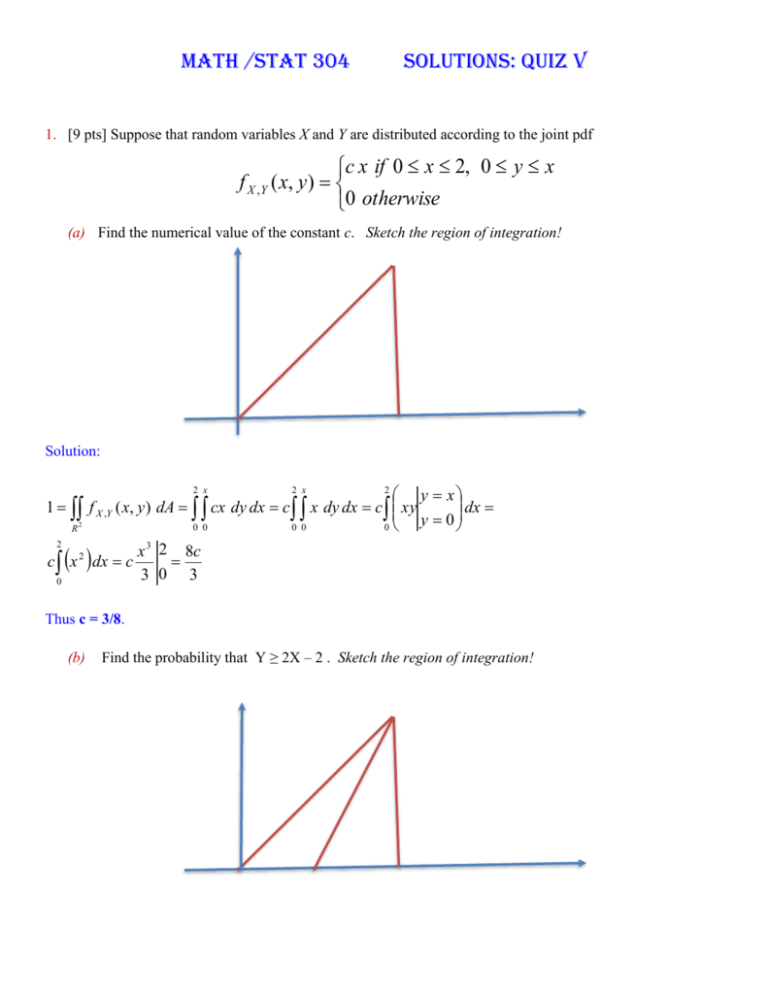



Math Stat 304 Solutions Quiz V




Solved For Each Of The Following Find Dy Dx Y X 3 E X Chegg Com




Chapter 7 Properties Of Expectation Question 4



If Y X Y X C Show That Dy Dx Y X Y 2 X 2 1 Sarthaks Econnect Largest Online Education Community



Find The Particular Solution Of The Differential Equation Dy Dx 1 X Y Xy Given That Y 0 When X 1 Sarthaks Econnect Largest Online Education Community




Dy Dx 2ytanx Sinx Y 0 When X P 3




Solved 13 Find The Value Of The Line Integral 4xy Dx 2x2 2y2 Dy Where C Is An Ellipse 1 From 3 0 0 2 Hint If X Y 4ryi 2x 2y Is Conservative The




Solve The Differential Equation Xsin Y X Dy Ysin Y X X Dx



Engineering Purdue Edu




Engineering Mathematics Notes



If Sin X Y Log X Y Then Dy Dx A 2 B 2 C 1 D 1 Sarthaks Econnect Largest Online Education Community



C Find Dy Dx And Simplify The Result If Possible Gauthmath




For The Differential Equations Given Find A Particular Solution Satisfying The Given Condition Dy Dx 3ycotx Sin 2x Y 2 When X Pi 2 Mathematics Shaalaa Com




How To Take The Derivative Of X 2 Steps Tutorial Video Lesson Transcript Study Com




Solved Example 4 A If Z F X Y X 4xy Find The Differential B If X Changes From To 2 05 And Changes From To 2 96 Compare The Values Of Az And




Ipe Material Notes




Answered Theorem If The Equation F X Y C Bartleby




Multivariable Calculus If X Y Y X Z Z C Then Find Frac Partial 2z Partial X Partial Y At X Y Z Mathematics Stack Exchange



How To Solve This The Gradient Of The Normal To A Curve At Any Point Is Equal To The X Coordinate At That Point If The Curve Passes Through The Point E 2 3 Find




Differentiating Related Functions Intro Video Khan Academy



X X X Y Y Video Song Download




1a Find Dy Dx X Te Y T Sin T B Find Dy Dx And Homeworklib




Example 25 Find Dy Dx If Y Sin Y Cos X Chapter 5 Class 12




Solved Section 3 1 6 9 16 25 Section 3 2 7 11 15 Chegg Com



4 If X 19 Cdot Y X Y 4039 Then Frac Dy Dx 17 Sep Shift I A 0 B Frac X Y C Frac Y X D 1 Snapsolve




Differentiability And Continuity Video Khan Academy




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




Examples 1 Math 2650 Calculus Of Variations Examples 1 The Practice Questions Marked P Will Be Studocu



How To Find Y As A Function Of X Given That Dy Dx 5 X 4 And That Y 12 When X 5 Quora




The Solution Of Y X 5 Dy Y X 1 Dx




167 If X 2 3 Y 2 3 A 2 3 Then Frac Dy Dx Is Equal To A Sqrt 3 Frac Y X B Sqrt 3 Y X C Frac Y X D None Of These Snapsolve




Engineering Mathematics Notes




If Y Log10x Then Dydx Maths Questions



Answered 2 Find The General Solution Of X Y Bartleby



Solved Solving 2 Ordinary Differential Equations Course Hero



What S The Solution Of The Linear Differential Equation 1 X 2 Dy Arctan X Y Dx Quora




Solved Erample That Shows It Is False 87 If F X X Then F X G X If F X G X C Then F X 8 X If Y 7r Then Dy Dx 2t 90 Ify



Solved Find Dy Dx A Y X 2 B Y X Y 2 C Y X X Chegg Com




Find Dy Dx If X Y C




The Maximum Minimum Values Of The Function Y X 3 3x 2 6 1 2 0 2 6 0 3 6 2 4 4 2 Pct6wwss Mathematics Topperlearning Com
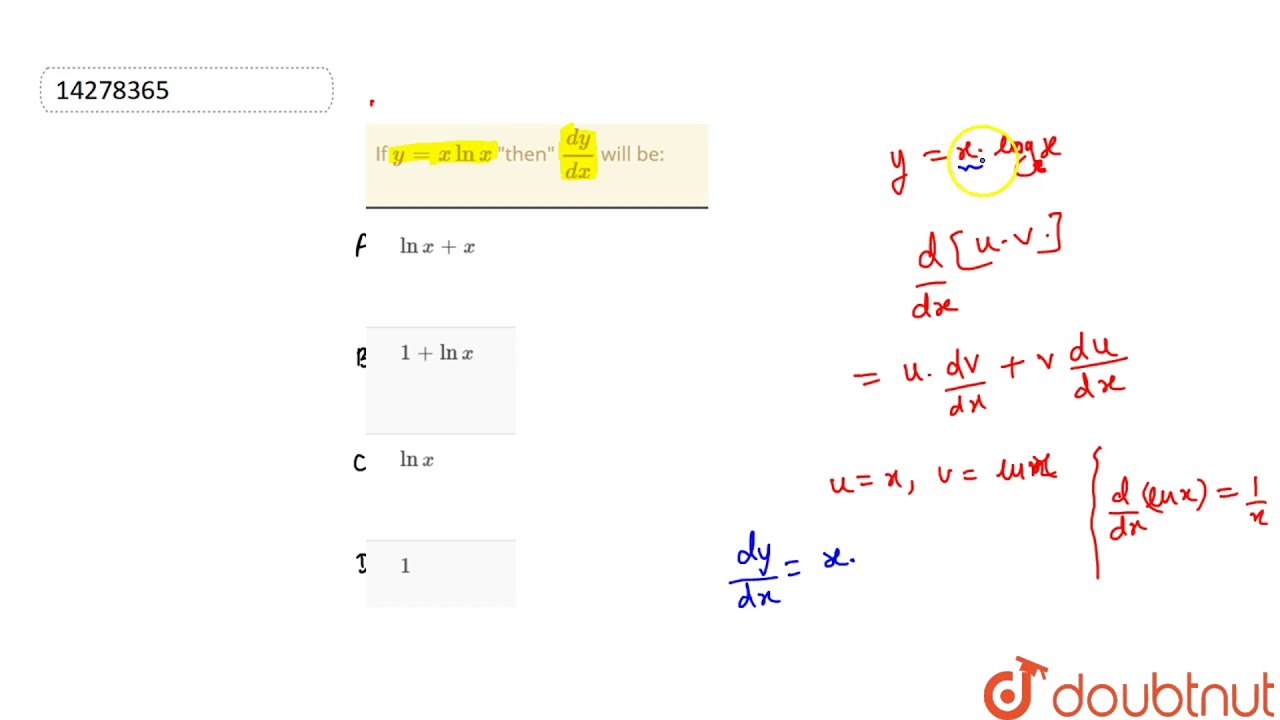



If Y X Lnx Then Dy Dx Will Be Youtube




Engineering Mathematics Notes



1




0 1 X




Misc 14 If X Root 1 Y Y Root 1 X 0 Prove Dy Dx Miscellaneou



I If Y X X X To C Show That Frac Dy Dx Frac Y 2 X 1 Ylog X Snapsolve




Solved Find The General Solution To Sin X Dx Cos X Y Cos 2 X Y X Cos C Sin A X Find The Unique Solution That Satisfies The Initial Condition Y N 2 3 Y X For This




Answered X To The Power Y Y To The Power X A To The Power B Then Find Dy Dx Brainly In



Solved Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1 Determine Y When X 2 Find The Differential Equation Of The Famil Course Hero



Lambert W Function Wikipedia




Determine The Value Of C That Makesthe Function F X Y Ce 2x 3y A Joint Probability Densityfunction Over Homeworklib



Exponentiation Wikipedia




Example 24 Find Dy Dx If X Y Pi Chapter 5 Ncert Examples



2



Find Dy Dx When X And Y Are Connected By The Following Relations Sarthaks Econnect Largest Online Education Community



0 件のコメント:
コメントを投稿